Introducción
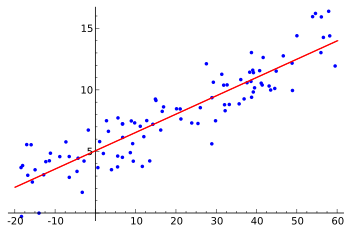
Los modelos de regresión son una herramienta fundamental en el aprendizaje automático supervisado. Se utilizan para predecir valores numéricos basados en datos de entrenamiento, donde las características (variables independientes) se relacionan con etiquetas conocidas (variable dependiente).
El proceso de entrenamiento de un modelo de regresión implica varias iteraciones en las que se ajustan algoritmos y parámetros para mejorar la precisión de las predicciones. Esto permite encontrar una función que relacione las variables de entrada con las de salida de la mejor manera posible. La regresión no solo se aplica a problemas simples de predicción, sino también en escenarios más complejos donde múltiples variables interactúan.
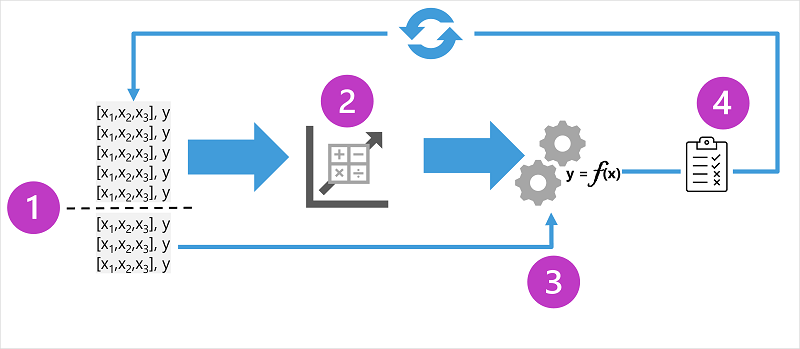
1. Proceso de Entrenamiento y Evaluación de un Modelo de Regresión
El entrenamiento de un modelo de regresión implica los siguientes pasos:
- División de datos: Separar un conjunto de entrenamiento y un conjunto de validación.
- Selección del algoritmo: Elegir un modelo adecuado, como regresión lineal, polinómica o modelos más avanzados como regresión con regularización (Lasso, Ridge).
- Entrenamiento iterativo: Ajustar el algoritmo a los datos de entrenamiento en múltiples iteraciones, mejorando la precisión en cada paso.
- Validación: Evaluar la precisión del modelo con los datos de validación y detectar posibles problemas de sobreajuste.
- Ajuste de parámetros: Refinar hiperparámetros mediante técnicas como validación cruzada o búsqueda en cuadrícula para mejorar la generalización del modelo.
2. Entrenamiento Iterativo y Optimización del Modelo
El entrenamiento de un modelo de regresión no ocurre en un solo paso; requiere un proceso iterativo donde se optimizan los coeficientes y los hiperparámetros. Algunas técnicas clave incluyen:
- Descenso de Gradiente: Método que ajusta los coeficientes iterativamente para minimizar la función de error.
- Regularización: Técnicas como Lasso y Ridge ayudan a reducir el sobreajuste penalizando coeficientes grandes.
- Aumento de Datos: En algunos casos, agregar datos sintéticos o transformar los existentes mejora la precisión del modelo.
- Selección de Características: Identificar las variables más relevantes para evitar ruido en los datos y mejorar la eficiencia del modelo.
3. Ejemplo de Regresión
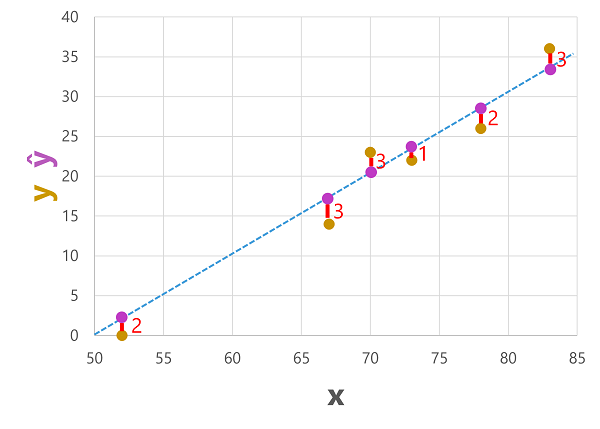
Para ilustrar el concepto, consideremos un modelo de predicción de ventas de helados basado en la temperatura:
| Temperatura (°C) | Ventas de Helados |
|---|---|
| 51 | 1 |
| 67 | 14 |
| 70 | 23 |
| 75 | 26 |
| 81 | 30 |
| 83 | 36 |
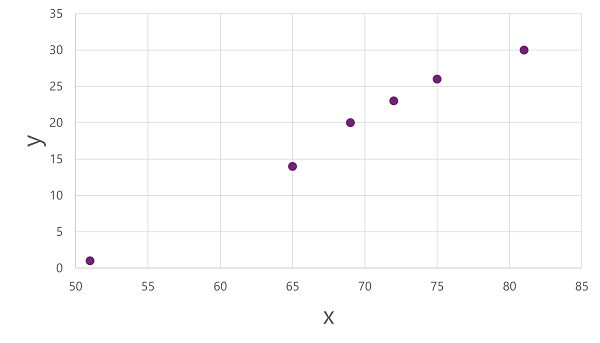
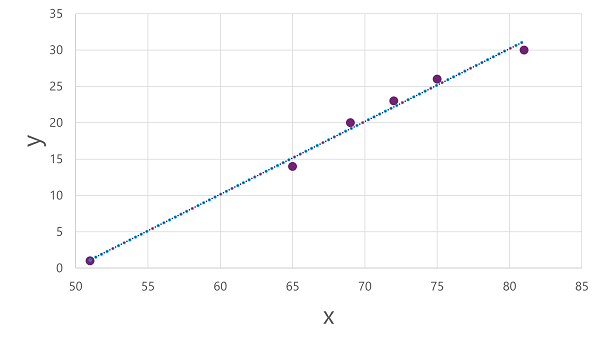
Aplicando regresión lineal, encontramos una función de ajuste:
f(x) = x-50
Esta función nos permite predecir la cantidad de helados vendidos según la temperatura del día. Sin embargo, en problemas del mundo real, podríamos necesitar modelos más complejos con múltiples variables.
4. Evaluación de un Modelo de Regresión
Para medir la precisión del modelo, utilizamos métricas de evaluación:
- Error Medio Absoluto (MAE): Promedio de los errores absolutos.
- Error Cuadrático Medio (MSE): Promedio de los errores elevados al cuadrado.
- Raíz del Error Cuadrático Medio (RMSE): Raíz cuadrada del MSE, interpretado en las mismas unidades que la variable dependiente.
- Coeficiente de Determinación (R2): Indica la proporción de la varianza explicada por el modelo.
Además, se pueden utilizar técnicas como curvas de aprendizaje y validación cruzada para evaluar la estabilidad y capacidad de generalización del modelo.
Conclusión
La regresión es una técnica poderosa en el aprendizaje automático, permitiendo hacer predicciones numéricas con alta precisión. Comprender su proceso de entrenamiento, validación y evaluación es clave para desarrollar modelos robustos y confiables. La optimización iterativa y el ajuste de hiperparámetros son esenciales para mejorar el desempeño del modelo en escenarios del mundo real.